Got time?
If you pay attention, you'll notice clocks are all around us. These relics of the past are present on city streets, town squares, church steeples, and stately university buildings. While they're all around us, few, if any, people who come across these devices know how to decipher their cryptic interface to actually read the time. We buy watches with analog dials to wear as fashion statements, often forgetting that they were initially created as timekeeping devices.
I'm here to help you attain the time-reading proficiency of a 19th-century railroad dispatcher!
Not what you expect
At first glance, telling the time looks trivial. For instance, take a look at this clock face:
What time is it? 2:10, right? Or perhaps 2:05:10? Or 5:02:10?
Surprisingly, the answer is none of these. In fact, the clock registers a time of 10:10:25 even though the largest indicator is pointing to 2 and there is no 25 to be seen.
Cryptic, eh?
The mystery
Over the years, I noticed that some of my cars had two clocks: an easy-to-read digital clock and an analog clock.
While the analog clock was clearly intended as a decorative flourish rather than a functional time-telling device, it appeared operational, so I decided it was time to figure it out.
Sadly, the 398-page manual for the car was of no use. It briefly identified the presence of the clock but said nothing about how to interpret its cryptic display.
The supplemental 190-page manual for the car’s infotainment system was equally unhelpful. It provides instructions for setting time zones, daylight saving time, and even whether time should be displayed automatically—but not how to actually read the clock. Apparently, Mercedes assumed that would be too obvious. They were wrong.
Watch instructions
I then thought an instruction booklet for a wristwatch might help. After all, if anything should explain how to read the time, it would be a device built solely for that purpose.
No luck there.
Rolex manuals graciously identify an “hour hand,” a “minute hand,” and a “seconds hand,” before breezily instructing: “to set the hour and minute, turn the crown.” That’s it. No guidance on how to verify that you’ve actually succeeded in setting it correctly.
Surely the luxury tier would help? I turned to the manual for the Patek Philippe Cubitus. After studying all 85 pages, I found only directions for winding and calendar adjustments. Apparently, when you pay $100,000 (before the oppressive 39% tariffs in the U.S.), they assume you already know how to tell time. Perhaps company sets up individual hands-on tutorial sessions. I wasn’t about to spend the money to find out.
Figuring it out
It couldn’t be that difficult to read the time. If 19th-century milliners could learn to do it, so could I.
Fortunately, the analog clock in my car is synchronized (I hope) to the GPS receiver, which also drives the digital display. That creates a Rosetta Stone of sorts: the digital display is the truth, and the analog display is the puzzle. By comparing the two, I could crack the code.
The Apple Watch offers the same kind of aid. It keeps one authoritative internal time and can display it in either digital or analog form. The time isn't synchronized from a GPS receiver but rather with the iPhone, which synchronizes from Apple's time servers via SNTP. The accuracy doesn't matter to me so long as the same time is reported regardless of the display. By toggling faces, one can observe the mapping between mysterious rotating sticks and neat digits.
Here we go!
Decoding the mystery
Now that we can compare the two representations, we can step through the elements that make reading a clock cryptic.
1. The shortest hand is the most significant
One might expect the more prominent clock hand to indicate the most significant element of the current time: the hour. Surprisingly, that's not the case. The shortest hand is the hour hand. The long hand is the minute hand.
Many watches and clocks have an additional long hand that indicates seconds. Its length is usually similar to the minute hand, and the hands are distinguished by their width and/or color. The hand that indicates seconds is almost always the thinnest. On some clocks, the second hand may be a different color from the hour and minute hands.
To summarize: the largest hand is not the most significant, the shortest hand is, and you’ll need both length and width cues to tell them apart. This is the opposite of good user interface design.
2. A 12-hour scale
Let's focus on the hour indicators. A clock dial has 12 hour markings, ideally numbered 1-12.
This forces the subdividing the day into two 12-hour periods, partitioning the first 12 hours into an ante meridiem group, sometimes abbreviated as a.m.) and the remaining 12 hours into a post meridiem group, sometimes abbreviated as p.m. This partitioning is familiar to most people and the terms are sensible as every minimally educated person has a basic understanding of Latin. Nothing says “clarity” like medieval clerical jargon.
The confusion stems from the fact that clocks provide no indication of the time period. 3:00 and 15:00 look exactly the same. You just have to know.
3. It's Latin to me
Many clocks insist on using Roman numerals. This offers no advantage beyond encouraging us to continue to use this numbering system. It originated from European inertia to change, which evolved into a global horological tradition.
While Indo-Arabic numerals started to gain use in the ninth century, it took a long time for them to gain widespread adoption. They got a boost after the publication of Fibonacci's book Liber Abaci in 1202.
For instance, in 1299, bankers and merchants in Florence were forbidden to use Indo-Arabic numerals by merchants was forbidden, primarily to prevent forgery and the ease of altering documents by interchanging numbers, especially the digits 6, 9, and 0. Some people were reluctant to adopt Indo-Arabic numerals because they had a hard time grasping the legitimacy of the number zero.
Almost universally, clocks with Roman numeral dials use IIII for the number 4 instead IV. One explanation is that this is done to avoid mistaking it for VI, the number 6, since the number its oriented upside down. The more dominant, and more likely, explanation is that this was done for symmetry -- to provide a better balance with VIII, 8, on the other side of the dial.
4. Missing numbers
Some clock faces provide clear indications of hours. Most do not. One or more numbers may be missing.
In some cases, there's a single missing number in a sequence to accommodate a date window or other marking. In other cases, multiple numbers may be missing. Some clocks make matters worse by omitting numbers altogether.
In the case of missing numbers, you will need to determine them yourself in real-time. If a single number is missing, you can interpolate. E.g., 3 must be between 2 and 4. If multiple numbers are missing, you may be able to identify and count the hour markers from the 12 o'clock position.
Alternatively, you can identify the position of an hour by visualizing the angle between a vector pointing to the 12 o'clock position and a vector pointing to an hour. The hour marker position is located at:
\[hour = \theta \div 30\]
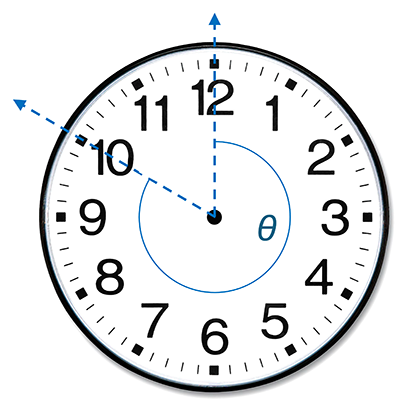In practice, people just squint and guess.
5. Three indicators sharing one dial face
One face, multiple meanings. The hour, minute, and second hands all pile onto the same circle, with no unique markings for minutes or seconds.
This leads to the problem of missing markings. While many clock faces will indicate at least some hours, most will not identify minutes or seconds.
This is something you have to compute from the hour markings. A full revolution (360°) of the minute hand represents the passage of one hour; hence, 60 minutes. Knowing that a full revolution (360°) of hours covers a span of 12 hours and that a full revolution of the minute hand covers 60 minutes, we can compute a conversion from the dial indicator of hours to a value in minutes:
\[minute = (hourmark \bmod{12})\times 5\]
For example, looking at the example at the start of this article, when the minute hand is at the 2 hour position, that represents \(2 \times 5\), or 10 minutes from the hour. That partially unravels the mystery: the hour hand points to 10 and the minute hand points to 2, making the time 10:10 (although we have no clue whether it's 10:10 or 22:10 since we cannot tell if we are ante or post meridiem). Note that we need to apply mod 12 to the hour so that 12 will be treated as 0.
Since there are 60 seconds in one minute, the same formula applies to the second hand, which makes a complete rotation in one minute. In that example, we saw the second hand was pointing to the 5-hour marking, which represents \(5 \times 5\), or 25 seconds after the minute. Hence, the clock reads 10:10:25. Mystery solved!
Or at least, mystery deferred until we notice the hands rarely line up neatly with these markings…
6. In-between positions for minutes
Most of the time, a minute hand will not be so obliging as to align perfectly with one of the hour markers. To account for this, many clocks add small ticks between the numbers. There are usually 4 short ticks between each pair of hour markings, dividing the 30° arc into five equal steps of 6°. Each step corresponds to one minute.
This means that if the hand is one tick past the "2," then instead of simply reading "10 minutes," the actual value is 11 minutes. Two ticks past makes it 12 minutes, and so on until the hand has traveled all the way to the next hour marker, at which point you must remember to reset your counting and start over again.
If the clock face has no ticks, the problem becomes more severe. You are then required to visually interpolate the hand’s angle between the larger markings. This is, of course, subjective and prone to error. Without intermediate ticks, your only options are (a) accept that you can only read minutes in multiples of five, or (b) attempt on-the-fly trigonometry to calculate the angular displacement relative to the nearest hour marker. Neither is particularly satisfying, but it explains why people have been late for centuries.
In summary: if ticks are present, count them; if they’re absent, guess.
7. In-between positions for hours
Take a look at this reading:
We can decipher the minute value as \[(6 \bmod 12) \times 5 = 30\] and we can compute seconds as \[(12 \bmod 12) \times 5 = 0 \times 5 = 0\]
Then we get to the hour hand. It's not pointing to any of the hour markings but rather sits between the 8 and 9 positions. Is the time 8:30:00 or 9:30:00 or something like 8.5:30:00??
As explained, the hour hand is coupled to the minute hand. The farther the minute hand has traveled around the dial, the farther the hour hand creeps toward the next number. That means the hour hand is a fuzzy indicator whose true value depends on the minute.
Let’s finish the second example:
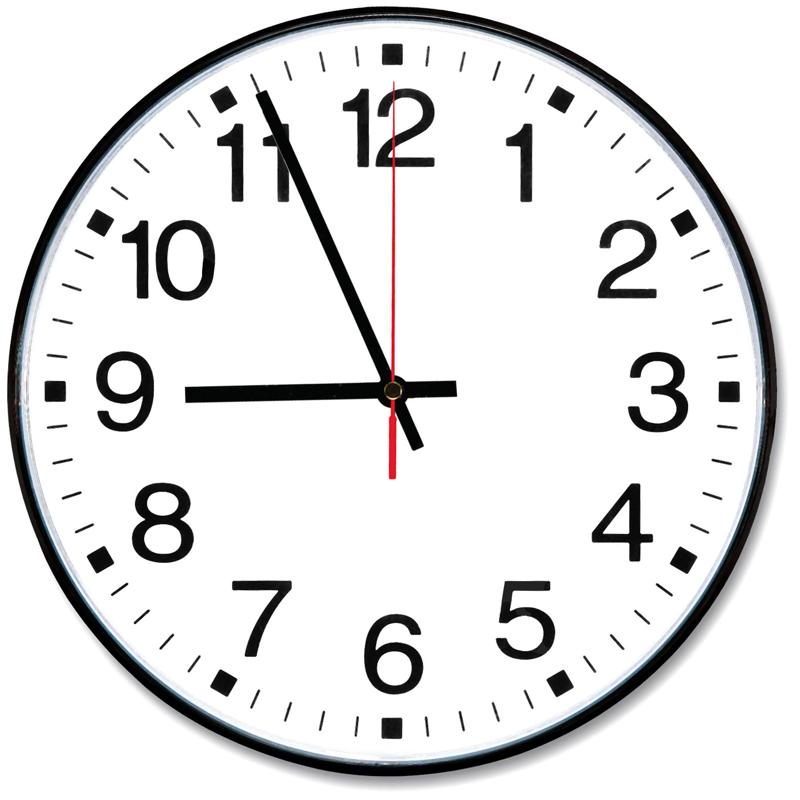
The hour hand looks suspiciously close to 9. A careless observer might announce the time as 9:56. But this is where discovery comes in. The minute hand is at 56 minutes, which is \(\tfrac{56}{60}\) of the way around the hour. Multiply this fraction by 30° (the angular distance between hour markings), and we see the hour hand has advanced \(28°\) toward the 9. That is almost, but not quite, at the next hour. Therefore, the hour value is still 8, even though the hour hand is almost kissing 9. The correct time is 8:56, not 9:56.
Thus the principle: if the hour hand is caught between two numbers, always round down to the earlier number. The creeping offset will only make sense once the minute hand has completed its journey and pulled the hour hand fully onto the next marker.
Conclusion
Through careful analysis, I have demystified the analog clock. It is not the straightforward, intuitive invention it pretends to be but a cryptic contraption requiring geometry, fractions, and a tolerance for ambiguity. The hands point where they do not mean, the numbers repeat twice a day, and Latin abbreviations add an unnecessary linguistic challenge.
And yet, once mastered, it becomes second nature. So second nature, in fact, that people stop realizing how bizarre it actually is. We glance, we mumble “quarter past,” and we go about our lives without once appreciating the mental acrobatics involved.
The next time you look at a clock tower or wristwatch, remember: you are not just “telling time.” You are performing analog trigonometry at a level that confounds many observers. Congratulations. You, too, are now qualified to dispatch trains in the 19th century or show up on time for afternoon tea!